Page 15 - ePD12207_升科大四技數學B領先講義含解析_課本PDF
P. 15
直線方程式 1
(3) 平行四邊形的頂點問題: 主
已知一平行四邊形 ABCD 的兩對角線 AC 、 BD 相交於O 點, 題
A
可得兩對角線互相平分性質,運用 O 點同時為 AC 、 BD 直角坐標、距離公式及分點坐標
x + x y + y x + x y + y
之中點特性,即O ( 1 3 , 1 3 ) = O ( 2 4 , 2 4 )
2 2 2 2
⇒ x + x = x + x 且 y + y = y + y ,亦即 AC+ = BD A(x , y ) 5
+
1
1
3
1
3
2
4
2
4
1
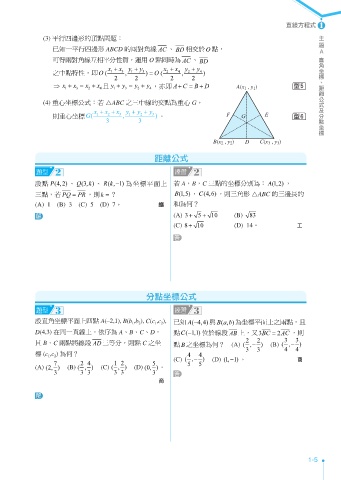
(4) 重心坐標公式:若 ABC 之三中線的交點為重心 G,
x + x + x y + y + y
則重心坐標G( 1 2 3 , 1 2 3 ) 。 F G E 6
3 3
B(x , y ) D C(x , y )
3
2
2
3
距離公式
2 2
設點 P(, )42 、 Q(,3 k) 、 Rk(,−1 為坐標平面上 若 A,B,C 三點的坐標分別為: A(, ) ,
)
12
15
46
三點,若 PQ = PR ,則 k = ? B(, ) ,C(, ) ,則三角形 ABC 的三邊長的
(A) 1 (B) 3 (C) 5 (D) 7。 [94 護 ] 和為何?
(A) 3+ 5 + 10 (B) 83
(C) 8 + 10 (D) 14。 [90 工 ]
分點坐標公式
3 3
, )
設直角坐標平面上四點 A(–2,1), B(b ,b ), C(c ,c ), 已知 A(−44 與 Ba b(, ) 為坐標平面上之兩點,且
1
2
1
2
D(4,3) 在同一直線上,依序為 A、B、C、D, 點C(, )−11 位於線段 AB 上,又3BC = 2AC ,則
2 2 3 3
且 B、C 兩點將線段 AD 三等分,則點 C 之坐 點 B 之坐標為何? (A) (,− ) (B) (,− )
標 (c ,c ) 為何? 4 4 3 3 4 4
2
1
)
7 2 4 1 2 5 (C) (,− 5 ) (D) (,11− 。 [98 商 ]
5
(A) (, )2 (B) (, ) (C) (, ) (D) (, )0 。
3 3 3 3 3 3
[101 商 ]
1-5