Page 21 - eAC20510_電工機械 上_課本PDF
P. 21
Chapter 1 電工機械基本概念 11
Σᔷνྡ 1–9(b) הͪfՉʕdᏨݴࠇܸ০ᔷ˙ΣʔΝdڌͪஹટᇞՇ၌ཥݴٙ˙
ΣʔΝf
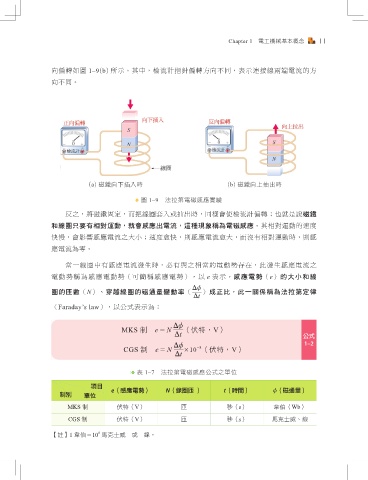
(a) 磁鐵向下插入時 (b) 磁鐵向上抽出時
圖 1–9 法拉第電磁感應實驗
ˀʘdਗ਼ှ᚛ո֛dϾҪᇞਸ਼ࢁɝאפ̈ࣛdΝᅵึԴᏨݴࠇᔷiɰఱ݊Ⴍ磁鐵
和線圈只要有相對運動,就會感應出電流,這種現象稱為電磁感應fՉ࿁༶ਗٙܓ
Ҟ࿔dึᅂᚤชᏐཥݴʘɽʃiܓฏҞdۆชᏐཥݴฏɽdϾӚϞ࿁༶ਗࣛdۆช
Ꮠཥݴމཧf
ɓᇞਸ਼ʕϞชᏐཥݴ೯͛ࣛd̀ϞၾʘٙཥਗැπίdϤ೯͛ชᏐཥݴʘ
ཥਗැ၈މชᏐཥਗැ̙ᔊ၈ชᏐཥැd˸ e ڌͪf感應電勢e的大小和線
Dz
圈的匝數N、穿越線圈的磁通量變動率 成正比,此一關係稱為法拉第定律
Dt
Faraday’s lawd˸ʮόڌͪމj
MKS 制 e = N Dz (伏特,V)
Dt ʮό
Dz 1–2
CGS 制 e = N × 10 (伏特,V)
-8
Dt
表 1–7 法拉第電磁感應公式之單位
ධͦ eชᏐཥැ Nᇞਸ਼̐ tࣛග zှஷඎ
Փйcc ఊЗ
MKS 制 伏特(V) 匝 秒(s) 韋伯(Wb)
CGS 制 伏特(V) 匝 秒(s) 馬克士威、線
8
【註】1 韋伯 = 10 馬克士威 或 線。